Special issue statement. This article is part of a special issue published on the occasion of the 70th anniversary of E&G Quaternary Science Journal (EGQSJ). The special issue celebrates the journal's notable contribution to Quaternary research by revisiting selected milestone articles published in the long history of EGQSJ. The German Quaternary Association (DEUQUA) presents translations of the originals and critical appraisals of their impact in tandem anniversary issues of DEUQUASP and EGQSJ, respectively.

Original article: https://doi.org/10.10.3285/eg.02.1.02

Tribute: https://doi.org/10.5194/egqsj-70-209-2021

Translators: Clare Bamford, Frank Preusser and Henrik Rother

This consideration leads us to examine the theoretically-expected stress on the ground that would be exerted by a stream of rigid individual bodies². We believe that a series of adjacent cuboid-like ice bodies is pushed forward along an inclined path by a force acting vertically everywhere (gravity) (Fig. 1). In each of the rigid cuboids, the force can be thought of as acting at the centre of gravity. This force can be deconstructed into two components, perpendicular and parallel to the surface. It follows, that in such a system, the steeper the underlying surface is inclined, the more of the downward pressure is transferred into the slope-parallel force components. At the same time, the force component acting vertically on the steep slope is equal for all participating bodies.

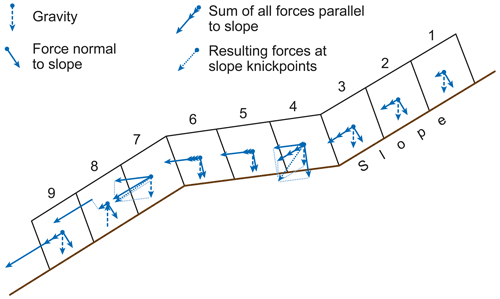
Figure 1Schematic sketch depicting the ground pressure of an idealized ice stream of rigid individual cuboid bodies at varying surface slopes. Note in particular the differences in size of the “force component normal to the slope” for cuboids 4 and 7 compared to the other cuboid blocks.

Download

A different picture, however, emerges for the cuboid bodies located at the foot of the steep slope, right at the transition to a flattening surface (block 4 in Fig. 1). In this case, a large part of the force transmitted parallel to the slope from uphill now suddenly takes part in the action perpendicular to the flattened underlying surface and is added as a strong additional component to the locally resulting force pressing at right angles to the ground. The next downward following cuboid, however, receives from above only the force component parallel to the ground in relation to the new ground inclination and shows only the right-angled part of the local vertical force as ground pressure.

One can also express the conditions in another way. As a result of the great ice rigidity and its relatively low ground friction, the inclined ice column over the steep slope rests on the foot of the slope, almost as if it were rigid. Here, a particularly strong stress will be exerted on the subsurface, and thereby erosion and undercutting.

Of course, ice is never completely rigid. In reality, the ice column lying on the slope thickens towards the bottom. But the fact that it does not flow completely apart until reaching a balance between the glacier surface above and below the steepened slope, and considering the relatively low friction at the glacier bed, forces us to conclude that a transfer of pressure through the ice column towards the foot of the slope takes indeed place.

From our concept of a moving flow of rigid individual blocks of ice, results the understanding of a significantly increased stress acting directly upon the foot of a slope. This theoretical result is also in agreement with the overdeepened troughs observed in glacially formed valley landscapes at the foot of cirque walls and valley steps. It is needless to add that such deepenings at the lee side of bedrock obstacles is ultimately limited in extent. This is because the developing counter-slope on the opposite (downvalley) side of the depression below the valley step, would eventually lead to such a strong increase in basal friction that the ice movement over the ground thus the erosion of the subsurface would decrease significantly.

Special conditions again exist at the upper cuboid ice body at the beginning of a new slope steepening (block 7 in Fig. 1). Here the force component transmitted from above and parallel to the upper, flatter slope now becomes a force directed away from the steepening slope towards the air. This additional force transmitted from above must therefore have an effect in form of a reduction in the ground pressure of this cuboid. Indeed, theoretically it could lead to the toppling of this cuboid from the support surface, which can also be seen in practice by imitating the described arrangement, e.g., with toy blocks.

This fact, too, is undoubtedly important for understanding the observational facts available on glacial erosion in valleys. Also, we consider it of considerable importance for explaining the formation of cirque and other sills (ridges) so often observed in glacial valleys, evidencing locally reduced ice erosion at the uppermost point of a slope.

Reduced ice erosion at the top of the steps and increased erosion at the foot of the steps are basic prerequisites for the theory of increasing pre-existing morphological bed irregularities by valley glaciers. By contrast, this theory is not compatible with the idea of glacier movement as represented by a viscous fluid. So far the issue has remained unresolved. The idea of glacier movement in the manner of a stream of rigid blocks, on the other hand, provides real justification for the assumptions underlying the glacial morphological theory for the interpretation of available observations. This seems to me to be its particular merit.

It seems necessary to point out that our ideas about the basal stresses of a flow comprising rigid bodies of ice slope knickpoints are essentially independent of whether or not the glacier block flow rests directly on its bed or if, according to the assumptions of Drygalski and modern glaciologists, a intermediate zone of greater plasticity occurs between the blocks and the glacier bed. Where the basal or wall pressure of the block floe flow is locally particularly high, as based on slope gradient or cross-sectional conditions, the intermediate zone of higher plasticity would either be squeezed away so that the rigid block touches the bed itself, or the plasticised masses would be pressed past such points with greatly increased speed. In both cases, there would be an increased stress on the bed wall at the points in question, at least according to all the previous experience of the effect of glacial ice on rock.

The idea developed by Ampferer (1904) that a glacier, especially in narrow valleys, is to be regarded as a rigid mass bearing down on the valley slopes on both sides with arch pressure and moving down the valley, is also not far removed from our idea of a block slab flow.

With the above stated ideas, we do not intend to suggest that a glacier as such constitutes a stream of rigid individual bodies. Rather, we seek to express that valley glaciers occupy a peculiar intermediate position between a viscous fluid and a stream of rigid individual bodies. In fact, glaciers appear to combine characteristics from both end members. According to the results of Finsterwalder (1950), they seem to behave more like viscous liquids when the ice moves slowly relative to the ice cross-section, and more like block floe flows when the ice moves relatively quickly. For the erosional capacity of valley glaciers, however, it is precisely the peculiarities corresponding to the analogy of a stream of rigid individual bodies, which have received less attention so far, and which are therefore of particular importance here.

The successes with regard to determining glacier volume and mass balance achieved for slow-flowing glaciers on the basis of velocity measurements and geometry leave little doubt that the glacier model of a viscous fluid comes very close to reality. Consequently, one should also conclude that glaciers of such type have only a modest sculpturing effect on their underground and will thus not enhance slope breaks on the valley floor.

The glaciers with block flow movement (detached blocks) behave differently. It appears to us that these glaciers of this type are the actual agents generating the stark variety of erosional landforms forms within glacial valleys. In my opinion, the above considerations contribute to coming closer to a theoretical understanding of their erosional power. Above all, however, I believe that our ideas may help to understand the apparent coexistence of relatively weakly erosional valley glaciers on the one hand and very effective glaciers on the other. By doing so, we seek to contribute to a reconciliation by giving credence to both of the currently existing positions in the discussion on glacier erosion.

The above considerations were mainly directed towards an interpretation of those peculiarities that occur in the longitudinal profile of valleys shaped by glacial erosion. However, they are also relevant for assessing the cross-sections of such valleys. It is not surprising that the more or less developed U-shape of glacial valleys represents the ideal cross-section form generated by an ice stream pushing over its bed with imperfect deformability, the rigidity of which, at least under certain, frequently realised conditions, is so great that the internal friction of the particles against each other is greater than the external friction against the bed and valley walls. These characteristics also mean that such a flow would not adhere equally firmly to the valley walls everywhere. Even at the terminus it is often found that the body of ice is only imperfectly in contact with the ground, so that its load and friction are only exerting effects on parts of its base.

According to the observations from glacier tunnels on the Marmolata by Handl (1917) and further reports on this by von Klebelsberg (1948), similar considerations should also apply to the upper firn field area. The important observations on the formation processes of roche moutonnée at the base of the upper Grindelwald glacier by Carol (1943, 1947) suggest that the contact pressure of ice, which varies from place to place during glacier movement over uneven ground, and is increased by the occurrence of pressure liquefaction and consequent increased plasticity of the ice, generally varies to a considerable extent. The overall result from assessing the interaction between a moving ice body with its bed and valley sides, which undoubtedly varies from place to place, must without question yield an explanation for the development of a U-shapes cross-section.

There has been much debate about whether the U-shape originates from a formerly V- or \__$/$-shaped valley cross-section, and if this was caused primarily by erosion on the valley side walls or the valley floor. It is difficult to give a general answer to this question. Certainly, cases of predominant vertical erosion and predominant lateral erosion can be realised side by side with varying frequency and intensity, without it being possible in every case to prove the predominance of one or the other (hence the suggestion of both possibilities in the ideal profile Fig. 2). On the one hand, the development of an overdeepened rock trough under a valley step in a glacial valley is unmistakable proof of strong vertical erosion of the glacier. However, there are also cases in which the bottom of a trough is filled with moraine material and a more V-shaped valley floor is largely maintained. In these cases, the formation of a trough is more likely to be due to erosion of the glacier on the valley sides. In view of the theory of glaciers enhancing pre-existing slope breaks, one may assume that the formation of a trough shape above a valley step is likely due to preeminent glacial erosion on the valley sides, whereas if this shape occurs at the foot of the valley step it is more likely due to a greater extent to vertical glacial erosion.

It seems appropriate to apply our ideas on the material consistency of glaciers also to investigate irregularities in the transverse profile of glacial valleys. We encounter these in features such as glacial trimlines (German “Schliffgrenze”), “Schliffkehle”, “Schliffbord”³ and rock scholder (“Trogschulter”). There is general agreement on understanding glacial trimlines as the upper limit of the ice flow moving laterally along the valley flanks and scouring it. However, less attention has been paid to the inherent consequences that can be derived from the specific range of land forms on or at the trimline. These, as is well known, comprise the following (Figs. 2 and 3):

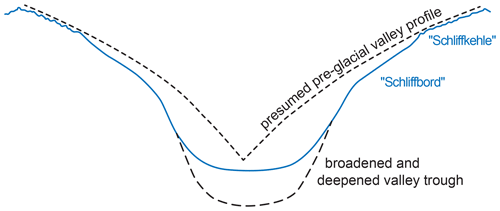
Figure 2Schematic cross-section of a trough valley with steep ice-moulded surfaces. Finely-dashed profile indicates the possible preglacial valley cross-section. Unbroken line of trough bottom corresponds to the assumption of shallow glacial erosion. Coarsely-dashed trough base corresponds to the assumption of a strong vertical component of glacial erosion.

Download

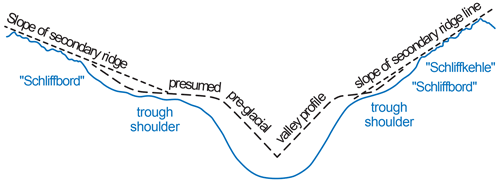
Figure 3Schematic transverse profile of a glacial trough with true trough shoulders. (The shoulder surfaces are shallower than the general ridge slope above the trimline. Their formation cannot be explained by the simple assumption of a gradual increase in glacial erosion from the trimline downwards. Roughly dashed: a possible form of the underlying preglacial valley profile showing trough terraces.)

Download

The ragged shape, resulting from subaerial weathering, of many secondary ridges which descend from the main ridge, take on a more rounded form from a certain altitude downwards. However, just above the point on the ridge where it transitions to a more rounded form, a noticeable steepening of the slope is usually discernible. As is well known, this finding prompted Albrecht Penck to give the name “Schliffkehle” to these features. However, as far as I know, it has not yet been clearly expressed that this finding can often be used to obtain information on the minimum size of the abrasive effect of the valley glacier moving roughly horizontally along the slope. This is possible when the mean slope of the ridge line of the secondary ridge above the gully steepening is so moderate that this ridge line experiences a clear bend through the recessed slope bend of the gully steepening (cf. Fig. 2).

Such sudden downshifting of the general hanging profile at the cut boundary is very common. The magnitudes involved usually range from several metres to tens of metres. They indicate the amount by which the abrasive action of the valley glacier moving along the slope at its upper margin has preceded the ablative action of subaerial weathering and denudation in the area rising above the glacier surface, thus producing the recessed angle on the slope.

The often-observed general lowering of the slope profile below the trimline shows that the so-called black-white boundary may play an additional but not a dominant role in the formation of the “Schliffkehle”. If the “Schliffkehle” was only a groove cut into the slope at the level of the ice flow, then the glacially shaped and polished surfaces below the trimline should approximately represent the imaginary lower continuations of the slopes above the steepening of the “Schliffkehle”. As a rule, however, they lie much lower than these imaginary continuations (cf. the suggestion of these conditions in Fig. 2).

From the appreciation of the high rigidity of the near-surface layers of the moving glacier ice, it could theoretically be concluded that in the glacial accumulation area, i.e., above the area of deposition of moraine material, the abrasive effect of the glacier must already begin at the valley margins with considerable force. In any case, there is little to suggest that the erosional effect decreases to zero towards the edge of the glacier, as could be inferred based on the concept of glaciers as a viscous fluid in which the speed of movement approaches zero towards the edge. Overall, the observations of the “Schliffkehle” indicate that glacial valleys were primarily formed by glaciers whose movement was of the block floe type or at least related to it.

If erosive processes by glaciers already commence at the high lateral valley sides (trimlines), then it must be assumed that erosion occurs with even greater effect at depth, in which ice mass are pushed along the walls and bed under yet greater pressure. Thus, in the transverse profile of the glacier bed, one can expect an increasing amount of erosion of the ice downwards along the valley walls to the bed. Yet, it cannot be determined whether the erosional maxima occur directly at the valley depth line, or if the maxima occur higher on the valley sides with the erosional capacity decreasing towards the depth line itself. As already discussed, both situations, that of predominant vertical erosion and that of predominant lateral erosion on the valley slopes, certainly do occur.

The idea of an increase in glacial erosion from the lateral margin into the depth of the central valley appears to be an important aspect for distinguishing between the entire ice-moulded area and the trough shoulder, which has not always been conducted with the desirable degree of attention. Quite often one finds broad, strongly inclined, smoothed surfaces developed below the ground grooves, which are noticeably flatter than both the steppened sections immediately above the “Schliffkehle” and the actual trough walls further down. In such cases, the question arises whether these features represent strongly over-printed pre-existing (old) valley floor remnants, i.e., genuine trough shoulders?

If we bear in mind that the probable cross-section of a previously straight or slightly convex slope (Fig. 2), reworked by a passing valley glacier, showing a steepening above the “Schliffkehle”, and then continuing below the “Schliffkehle” almost parallel to the original angle of slope, but again gradually steepening downwards, until it finally merges into the actual trough walls, we see the possibility of explaining such forms without the aid of postulating the presence of old valley floor remains. Especially when the slope of the rounded areas below the trimline, but above the trough walls, is as great or greater than the average slope of the slope or the crest line of the secondary ridges, which rise above the ridge caused by the groove boundary to the main ridge, there is no reason to think of old valley floor remains as the cause of these areas of more moderate slope above the actual trough walls. They are undoubtedly merely abrasion ridges, i.e., areas which have been removed by the ice flowing past, and which merge downwards into the trough walls as a result of the increased abrasion work of the ice. Von Drygalski (1912), Philippson (1912) and others have put forward a number of arguments for this. Such ice-moulded terrain, which to all appearances does not derive from old valley floor remains, is more frequent in the Alps than is generally assumed, as a closer examination of many slope profiles has shown to me. This is also indicated by von Klebelsberg (1948: p. 353).

Only when the ice-covered areas above the trough walls have a lower inclination than the slope above the trimlines, or than the ridge lines of the secondary ridges leading up from there to the main ridge (Fig. 3), is it possible to conclude with some certainty that old slope segments or valley floor remnants are present. In such cases they are real trough shoulders. The fact that such trough shoulders actually occur, even several of them on top of each other, and can be shown to be over-printed remnants of old valley floors, has been certain since the work by Lautensach (1912) in Ticino and has also been proven in many other cases.

But it seems to me that so far not enough attention has been paid to the distinction between two fundamentally different trough cross profiles: the true trough shoulder profile with rather flat shoulder surfaces and the ground slope profile with much steeper slopes above the actual trough. The trough shoulder profiles are most often found in glacial landscapes where pronounced altitudinal levels exist (“Gipfelflur”), with a middle or low relief at the top and abrupt valley notches below. The trough shoulder profiles are most often found in glacial landscapes with a pronounced vertical structure, with a middle or low relief at high altitude and abrupt valley thresholds below. Trimlines are found mainly in areas with high, moderately steep average slopes. If the slopes in deeply-eroded mountains are even too steep, the type of all-valley troughs described by Distel (1912) results from strong valley glaciation.

Here it should be pointed out that a trough profile with a steep ice-moulded area can be derived without further difficulty from the glacial reshaping of a previously existing simple groove or bed valley. This is based on the physically probable assumption that the erosion of the valley glacier starts at the trimline with a certain amount, that it initially increases downslope towards the base of the bed until it reaches a maximum, and that it can then possibly decrease again towards the centre of the bed. The deepening of the profile at the crevasse throat gives an indication of the minimum erosion work carried out by the glacier at the edge.

This paper was edited by Frank Preusser.